Calculus without limits

The history of mathematics is to an astonishing degree the history of calculus. The calculus was the first great achievement of mathematics since the Greeks and it dominated mathematical exploration for centuries.

In the beginning there were two calculi, the differential and the integral. The first had been developed to determine the slopes of tangents to curves, the second to determine the areas of certain regions bounded by curves.

Newton and Leibniz

The general idea of calculus, its fundamental theorem, and its first applications to the outstanding problems of mathematics and the natural sciences are due independently to Isaac Newton (1642-1727) and Gottfried Leibniz (1646-1716).

The methods developed by these two men solved the same class of problems and proved many of the same theorems yet were based on fundamentally different theories.

Newton thought in terms of limits whileas Leibniz though in terms of infinitesimals, and although Newton’s theory was formalized long before Leibniz’s, it is far easier to work with Leibniz’s methods.

Leibniz’s work as formalized by Abraham Robinson in 1961 under the name of nonstandard analysis.

The Infinitesimals

This approach to calculus involves expanding the real number system by introducing new numbers called infinitesimals.

These new numbers will have the property that although different from zero, each is smaller than every positive real number and larger than every negative real number.

Suppose we wantd to find the slope of the tangent to \(y=x^2\) at the point \((1,1)\)

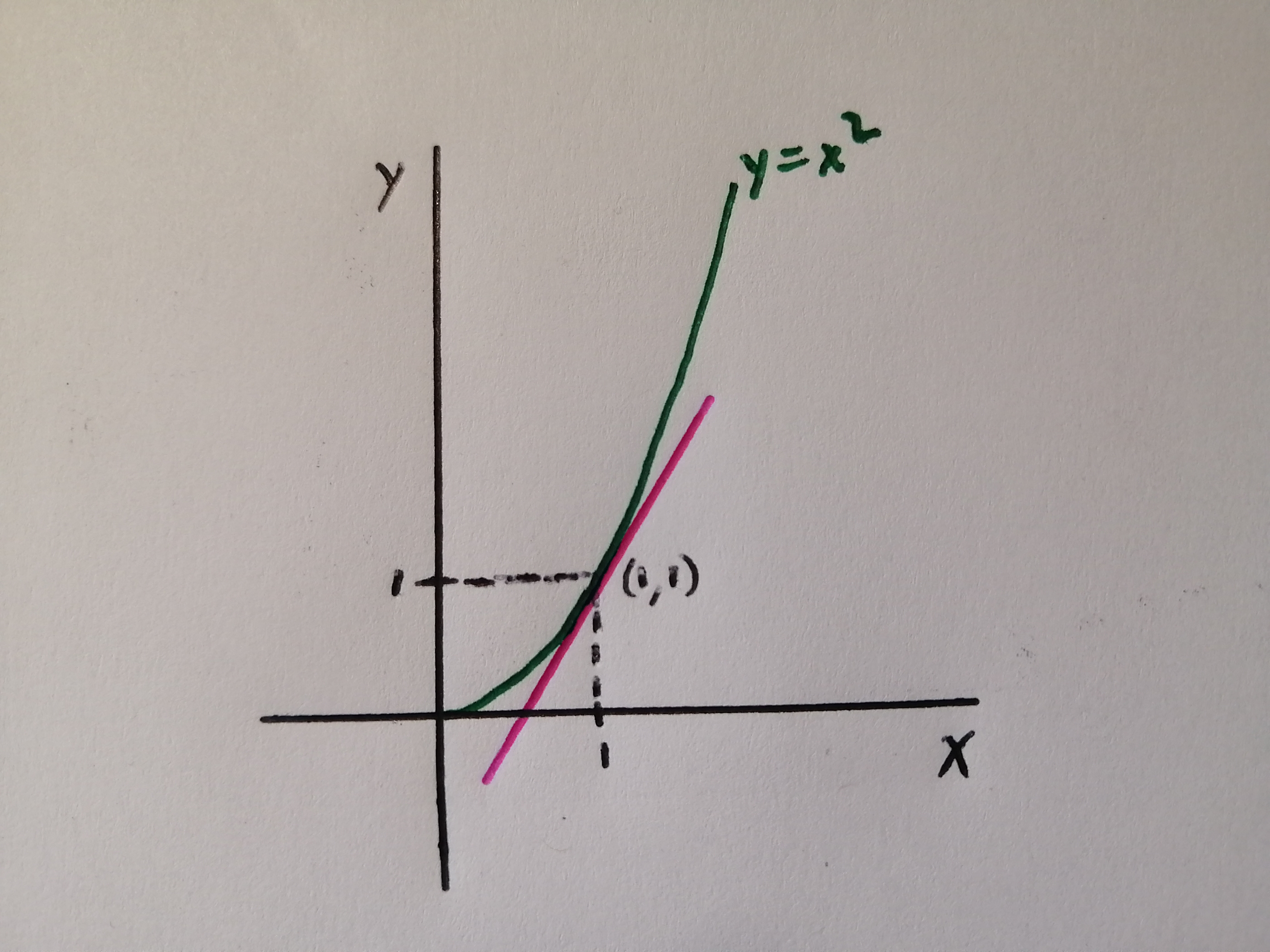
How can we approach this problem without the notion of limites?

We know how to find the slope of a line given two points of said line, but here we are only given one point \((1,1)\) plus the information that the line is tangent to \(y=x^2\) at that point.

1. Let \(\odot\) denote a positive infinitesimal.

2. Consider two points of the curve \(y=x^2\) which are infinitely close to one another, (1,1) and \((1,(1+\odot)^2)\)

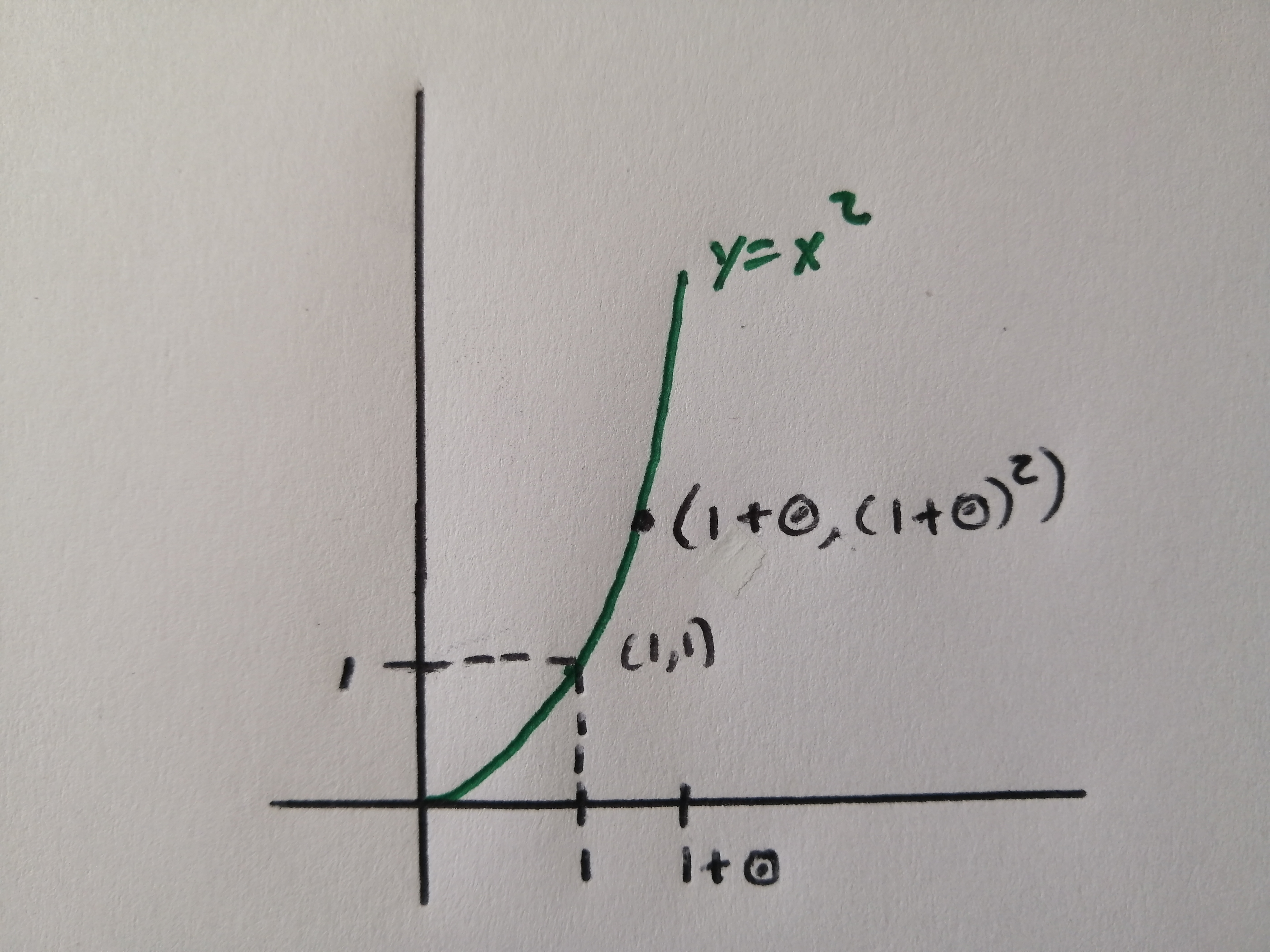
We can find the slope of the line going through these two points:

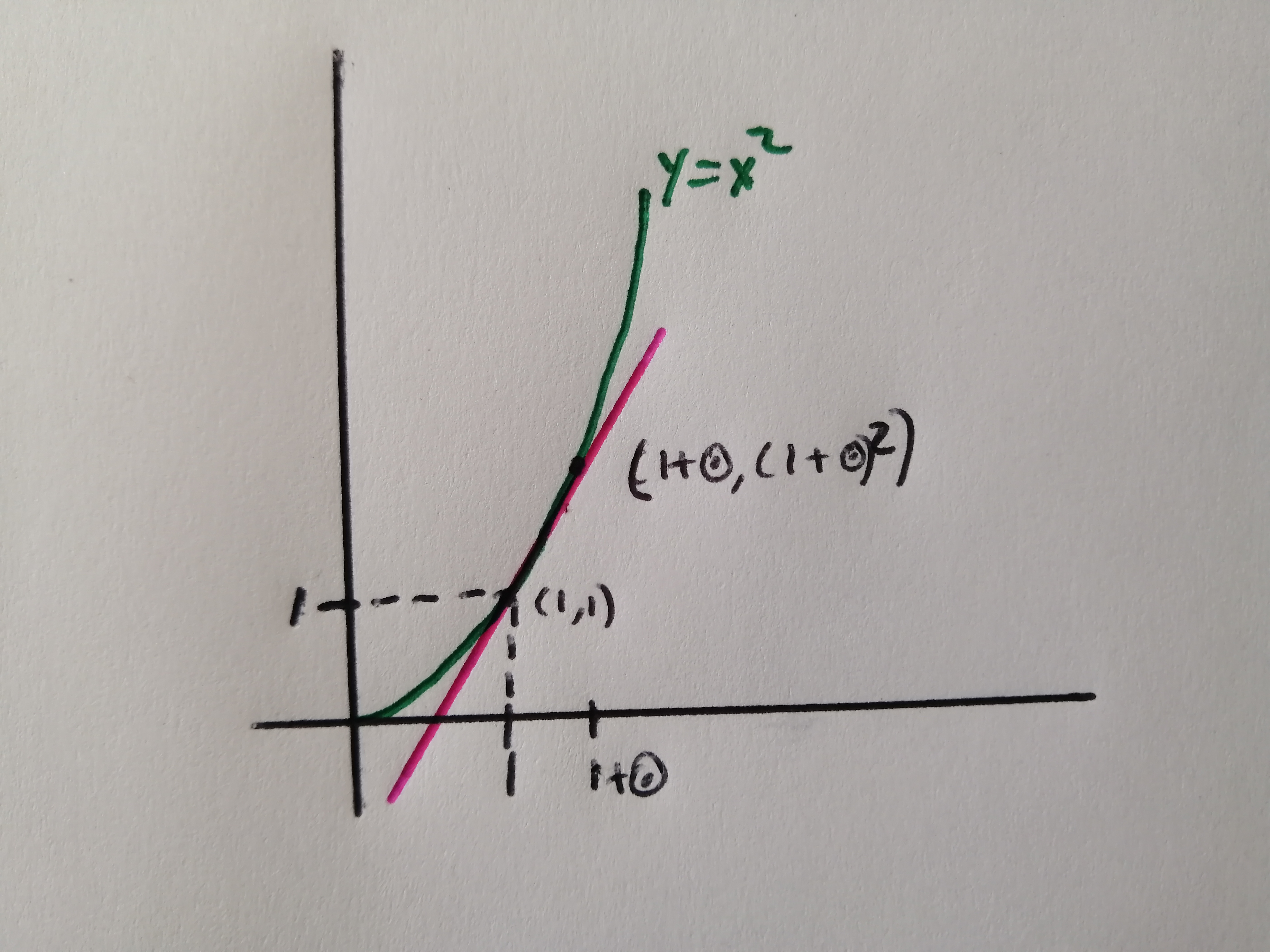
it is

\[\frac{\Delta y}{\Delta x}=\frac{(1+\odot)^2-1}{(1+\odot)-1}=\frac{\odot^2+2\odot}{\odot}=2+\odot\]

Similarly, the slope of the chord going through \((1,1)\) and \((1,(1-\odot)^2)\) is \(2-\odot\).

So what is the slope of our desired tangent? Well, the slope of the tangent must be a real number (\(2+\odot\) and \(2-\odot\) are not real numbers), and it must fall between the slope of the chords \(BA\) and \(AC\).

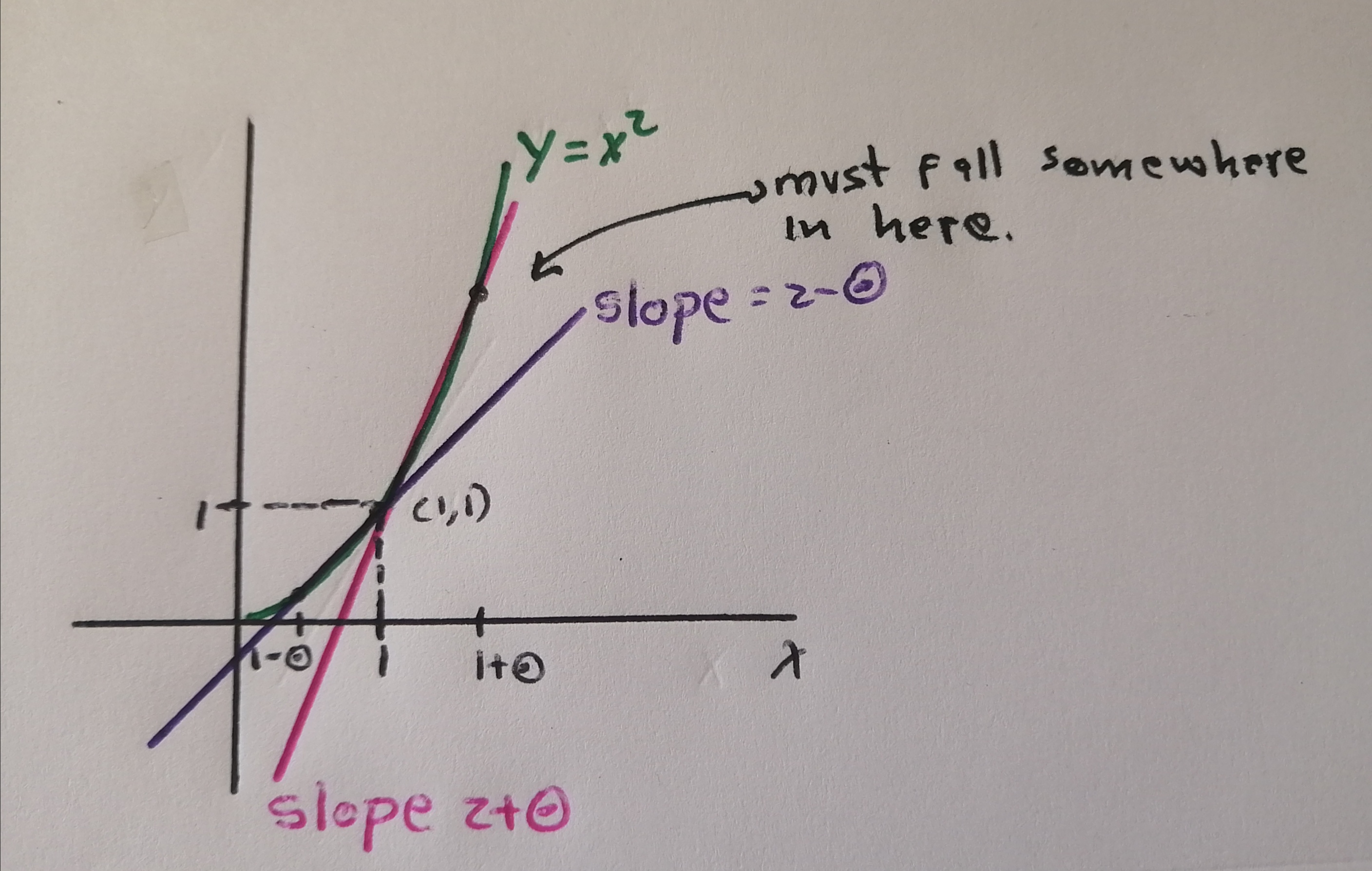
Two is such a real number, and it is easy to see that 2 is the only such number: Since \(0<\odot<r\) for every real \(r>0\), there can be no reals between 2 and \(2+\odot\), and similarly, since \(-r<-\odot<0\) for every real \(r>0\), there can be no reals between \(2-\odot\) and 2. Thus 2 is the only real number between \(2-\odot\) and \(2+\odot\), and so 2 must be our desired slope.

NICE!!!

For contrast, lets look at a Newton-style proof that the slope is 2: For any \(\Delta x\) the ratio \(\frac{\Delta y}{\Delta x}\) is an approximation of the true slope of the curve.

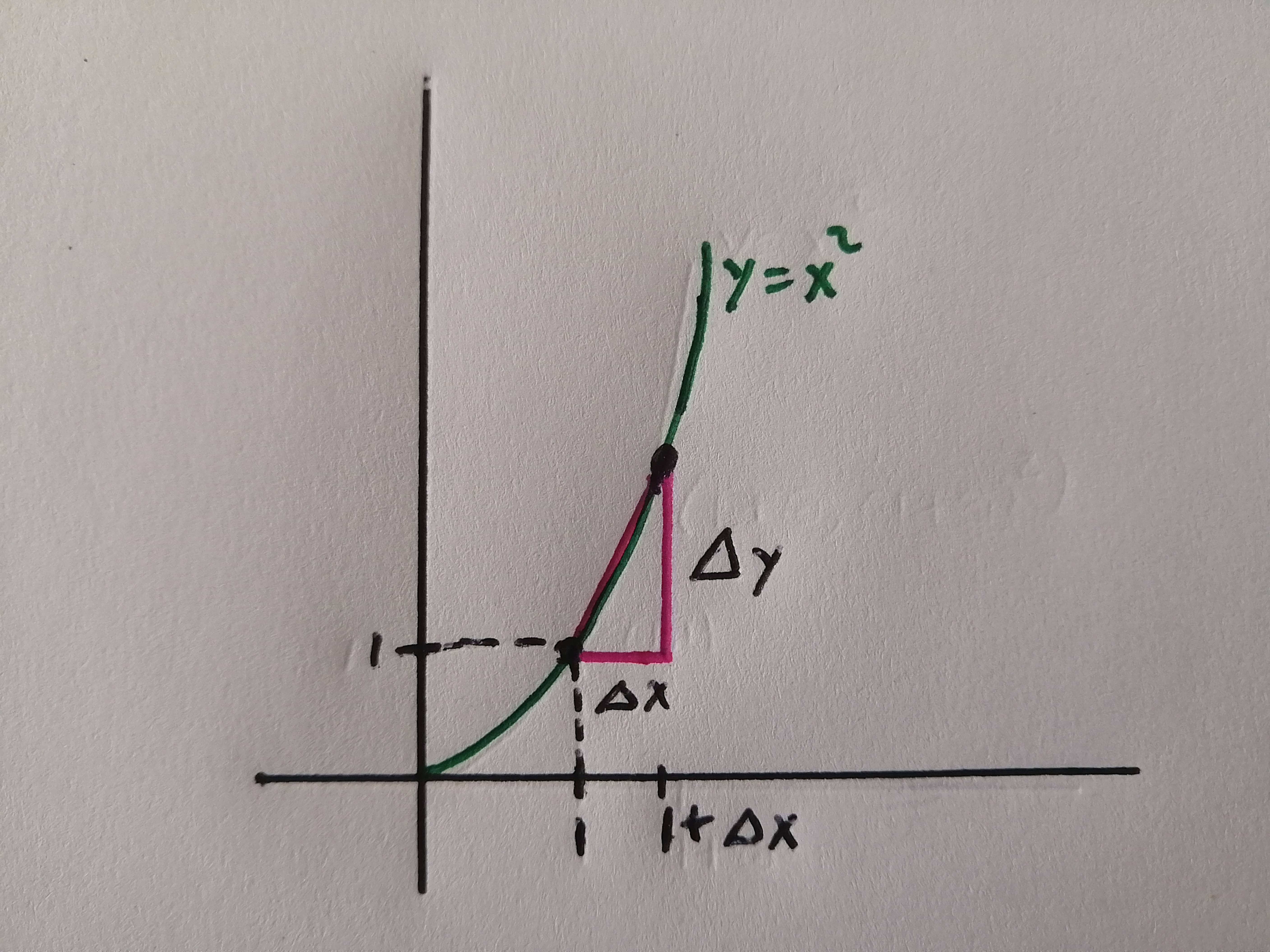
As \(\Delta x\) becomes smaller and smaller, the approximation improves, and the limit, as \(\Delta x\) approaches zero, is the desired slope.

To be precise, if \(f(x)\) is any function, we define the limit of \(f(x)\), as x approaches a, equals b as follows:

\(\lim_{x\rightarrow a}{f(x)}=b\).

And it reads:

For all \(\epsilon>0\), there is a \(\delta>0\) such that whenever \(0<\vert x-a\vert<\delta\), then \(\vert f(x)-b\vert<\epsilon\).

To apply this, we first define a function \(m(\Delta x)=\frac{\Delta y}{\Delta x}\). By calculations we find that given \(\Delta x\),

\(\Delta y\) is 2\(\Delta x+(\Delta x)^2\).

Thus \(m(\Delta x)=\frac{2\Delta x+(\Delta x)^2}{\Delta x}\).

Finally we prove that according to the definition of limit,

\(\lim_{\Delta x\rightarrow 0}{m(\Delta x)}=2\).

That is, for every \(\epsilon>0\), there is a \(\delta>0\) such that whenever

\(0<\vert\Delta x-0\vert<\delta\) then \(\left\vert\frac{2\Delta x-(\Delta x)^2}{\Delta x}\right\vert<\epsilon\)

The proof goes as follows: Suppose \(\epsilon>0\) is given. Then let \(\delta\) equal \(\epsilon\). We now check that this \(\delta\) works:

if \(0<\left\vert\Delta x-0\right\vert<\delta\), then

\[\left\vert\frac{2\Delta x-(\Delta x)^2}{\Delta x}-2\right\vert\]

\(=\vert2+\Delta x -2\vert=\vert\Delta x\vert=\vert\Delta x-0\vert<\delta=\epsilon\) \(\square\)

Notice that if \(\Delta x\) actually equals zero, then \(\Delta y=0\) too and \(m(0)=\frac{0}{0}\), which is undefined.

Written on December 11th, 2020 by José María Landa Chávez